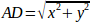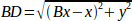Kinematics
Introduction
When we talk about CNC machines, we usually think about machines that are commanded to move to certain locations and perform various tasks. In order to have an unified view of the machine space, and to make it fit the human point of view over 3D space, most of the machines (if not all) use a common coordinate system called the Cartesian Coordinate System.
The Cartesian Coordinate system is composed of three axes (X, Y, Z) each perpendicular to the other two. [1]
When we talk about a G-code program (RS274/NGC) we talk about a number of commands (G0, G1, etc.) which have positions as parameters (X- Y- Z-). These positions refer exactly to Cartesian positions. Part of the Machinekit motion controller is responsible for translating those positions into positions which correspond to the machine kinematics. [2]
Joints vs. Axes
A joint of a CNC machine is a one of the physical degrees of freedom of the machine. This might be linear (leadscrews) or rotary (rotary tables, robot arm joints). There can be any number of joints on a given machine. For example, one popular robot has 6 joints, and a typical simple milling machine has only 3.
There are certain machines where the joints are laid out to match kinematics axes (joint 0 along axis X, joint 1 along axis Y, joint 2 along axis Z), and these machines are called Cartesian machines (or machines with Trivial Kinematics). These are the most common machines used in milling, but are not very common in other domains of machine control (e.g. welding: puma-typed robots).
Trivial Kinematics
The simplest machines are those in which which each joint is placed along one of the Cartesian axes. On these machines the mapping from Cartesian space (the G-code program) to the joint space (the actual actuators of the machine) is trivial. It is a simple 1:1 mapping:
pos->tran.x = joints[0];
pos->tran.y = joints[1];
pos->tran.z = joints[2];
pos->a = joints[3];
pos->b = joints[4];
pos->c = joints[5];In the above code snippet one can see how the mapping is done: the X position is identical with the joint 0, the Y posittion with with joint 1, etc. The above refers to the direct kinematics (one direction of the transformation). The next code snippet refers to the inverse kinematics (or the inverse direction of the transformation):
joints[0] = pos->tran.x;
joints[1] = pos->tran.y;
joints[2] = pos->tran.z;
joints[3] = pos->a;
joints[4] = pos->b;
joints[5] = pos->c;Non-trivial kinematics
There can be quite a few types of machine setups (robots: puma, scara; hexapods etc.). Each of them is set up using linear and rotary joints. These joints don’t usually match with the Cartesian coordinates, therefore we need a kinematics function which does the conversion (actually 2 functions: forward and inverse kinematics function).
To illustrate the above, we will analyze a simple kinematics called bipod (a simplified version of the tripod, which is a simplified version of the hexapod).
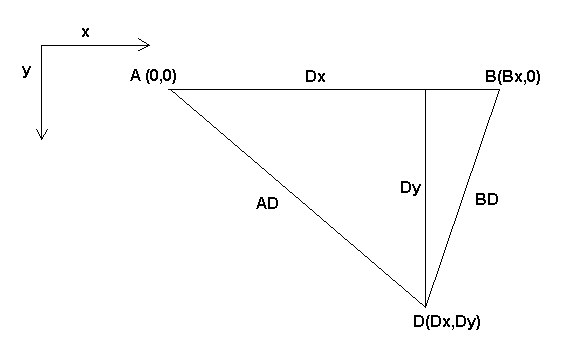
The Bipod we are talking about is a device that consists of 2 motors placed on a wall, from which a device is hung using some wire. The joints in this case are the distances from the motors to the device (named AD and BD in the figure).
The position of the motors is fixed by convention. Motor A is in (0,0), which means that its X coordinate is 0, and its Y coordinate is also 0. Motor B is placed in (Bx, 0), which means that its X coordinate is Bx.
Our tooltip will be in point D which gets defined by the distances AD and BD, and by the Cartesian coordinates Dx, Dy.
The job of the kinematics is to transform from joint lengths (AD, BD) to Cartesian coordinates (Dx, Dy) and vice-versa.
Forward transformation
To transform from joint space into Cartesian space we will use some trigonometry rules (the right triangles determined by the points (0,0), (Dx,0), (Dx,Dy) and the triangle (Dx,0), (Bx,0) and (Dx,Dy).
We can easily see that  ,
likewise
,
likewise 
If we subtract one from the other we will get:
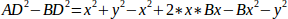
and therefore:
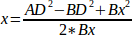
From there we calculate:
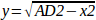
Note that the calculation for y involves the square root of a difference, which may not result in a real number. If there is no single Cartesian coordinate for this joint position, then the position is said to be a singularity. In this case, the forward kinematics return -1.
Translated to actual code:
double AD2 = joints[0] * joints[0];
double BD2 = joints[1] * joints[1];
double x = (AD2 - BD2 + Bx * Bx) / (2 * Bx);
double y2 = AD2 - x * x;
if(y2 < 0) return -1;
pos->tran.x = x;
pos->tran.y = sqrt(y2);
return 0;Inverse transformation
The inverse kinematics is lots easier in our example, as we can write it directly: